第2回目は、ディープラーニング(Deep Learning:深層学習)の概要と活性化関数について説明します。
ディープラーニング
ディープラーニングは、図1のように多数ニューロンを何層にも重ねたものです。ニューラルネットワークでは、出力層(n層)の出力と正解値を比較して、その誤差を出力層から入力層(0層)に向けて伝搬していくことで重みを更新します。この学習方法は「誤差逆伝搬法」と呼ばれています。例えば、0層目に顔画像を入力し、出力層で写っている人の年齢を推定するとします。出力値yiが20であったとすると、正解値の37歳との誤差は17となります。この誤差が小さくなるように誤差を伝搬して重みwを更新していきます。この誤差逆伝搬法による重みwの更新を繰り返すことで、正解値に近い出力が得られるようになります。
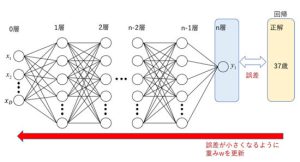
図1 ディープラーニングと誤差逆伝搬法
活性化関数
ディープラーニングとは-基礎知識(1.ニューラルネットワーク)で解説した通り、ニューラルネットワークは神経細胞を参考に考案された手法で、その概略図は図2の通りです。このニューロンを多数連結し、何層にも重ねたものが図1のディープラーニングです。
x1からx4 の入力に、重みw1からw4が掛け合わされ、入力信号の総和uが計算されます。そして、入力信号の総和uに基づいて出力信号zを出力します。総和uから出力zを求める関数は活性化関数f(u)と呼ばれています。数式で書くと、
u=w1x1 + w2x2 + w3x3 + w4x4+b
z=f(u)
です。この活性化関数f(u)は、生物の神経細胞が持つ性質と同様に、総和uが大きいときに大きな値を出力します。
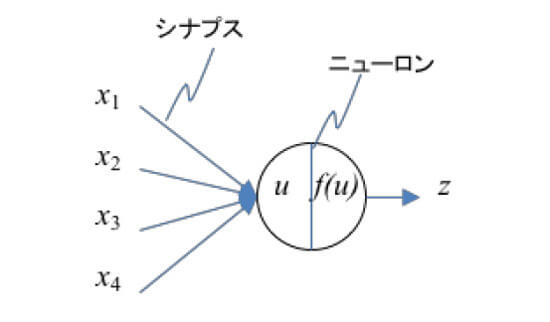
図2 各ユニットの入出力
活性化関数には、「ロジスティックシグモイド関数」、「双曲線正接関数」、「正規化線形関数」があります(図3)。正規化線形関数が、計算量が小さく学習速度も早いため、近年良く使われています。
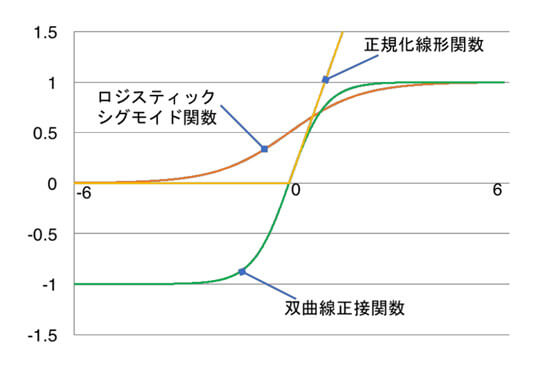
図3 代表的な活性化関数
また、前述の年齢推定のように連続値を求める場合は、1以上の連続値を出力する必要があるため、出力層の活性化関数に恒等写像z=uを用います。
次回は、「回帰」、「2クラス分類」、「多クラス分類」におけるディープラーニング(Deep Learning:深層学習)の出力層の違いについて解説します!
