第4回目となる今回は、学習のテクニックの1つである「ミニバッチ学習」について説明します。
まずは、ミニバッチ学習を説明するために必要なバッチ学習、オンライン学習を紹介します。
バッチ学習
これまでと同様に、学習データをx、正解データ(教師データ)をt、重みをwとします。そして、ディープニューラルネットワークをf(x; w)とすると、正解値tに対する 、f(x; w)による推定値yの誤差の大きさを表す損失関数は、L(t , x; w)と表記できます。学習では、この損失関数L(t , x; w)がより小さくなるように重みwを更新する処理を繰り返します。
バッチ学習では、N個の学習データ全てを用いて損失関数L(t , x; w)を求め、重みwを更新します。具体的には次式の通り、1つ1つの学習データから求めた損失Lの平均を求めます。
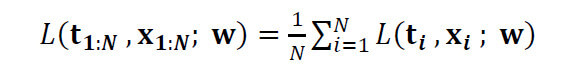
この平均値を学習時に用いる損失として学習処理を行い、重みwを更新します。バッチ学習では学習データの全ての情報を使用し、全体の誤差を直接最小化するため、多くの場合に安定した学習結果が得られます。また、重みの更新処理を一気に行えるため、学習処理を高速で行うことができます。
オンライン学習
オンライン学習(確率的勾配降下法)では、ひとつひとつの学習データごとに学習処理を行い、重みwを更新します。具体的には、N個の学習データx1、x2、…、xNからランダムに1つの学習データxiを抽出し、その1つのデータから求まる損失L(ti , xi; w)を用いて重みwを更新します。
オンライン学習では、1つの学習データのみをより正しく認識できるように重みを更新するため、1回の学習処理だけを考えると、選択された学習データ以外のデータについてはより正しく認識できるようになるとは限りません。学習データセットのサイズが大きく、それらが互いに独立していない場合、この学習処理を繰り返すことでバッチ学習よりもより良い結果が得られると言われています。また、オンライン学習ではランダムに学習データを選択するため、極小解に陥ってしまうリスクを低減できるという効果もあります。
ミニバッチ学習
ミニバッチ学習は、バッチ学習とオンライン学習の中間的な手法です。学習データをほぼ等しいサイズのグループに分割し、各グループごとに損失Lを計算し、重みwを更新します。つまり、N個の学習データをn個のデータからなるグループに分割したとすると、損失関数Lは
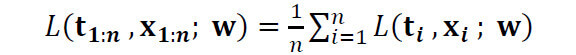
となります。
各グループのデータ数nは、10~100前後とすることが多いと言われています。ただし、分類したいクラス数に応じてデータ数nを決める必要があます。例えば、クラス数が50であれば、nは50以上とする方が良いです。これは、ミニバッチの中に各クラスに属するデータが最低でも1つずつ含まれるようにミニバッチを作成したほうが良いということを意味します。ただし、ミニバッチはランダムに生成しないと、オンライン学習で述べた「局所解に陥りにくい」という効果が薄れてしまうため、その点は注意が必要となります。
次回は、学習テクニックの1つであるデータオーグメンテーションについての解説です!
