第6回目は、ニューラルネットワークの学習の基礎知識である「勾配法」について紹介します。
ディープラーニングの基礎の第3回で説明した通り、教師データ(正解データ)と予測値との一致度を表す損失関数(誤差関数)を定義し、その損失関数が最小となる最適な重みパラメータとバイアスを自動的に求めます。この最適なパラメータを求めることが機械学習における学習です。パラメータ数は数千、数万を超えるため、手作業で最適値を求めることはほぼ不可能です。そのため、教師データから問題を解くために必要なパラメータを自動的に求められることが、ディープラーニング(Deep Learning:深層学習)を含む機械学習の大きなメリットと言えます。
勾配法
ディープラーニングを含む多くの機械学習では、先述の損失関数が最小となる最適なパラメータを求めることになりますが、一般的に損失関数は非常に多くのパラメータを含むため複雑な形となります。シンプルな方程式を解くような線形解法では解けない場合がほとんどです。そこで、損失関数がより小さくなるようなパラメータを繰り返し求めることで最適値を得るという方法を用いることになります。これが、勾配法と呼ばれる方法です(図1)。重みパラメータw=w1における損失関数の勾配を求め、その勾配を利用して損失関数の値がより小さくなるパラメータw2を求めます。勾配を求める際には、高校や大学で勉強した微分、偏微分が登場します。
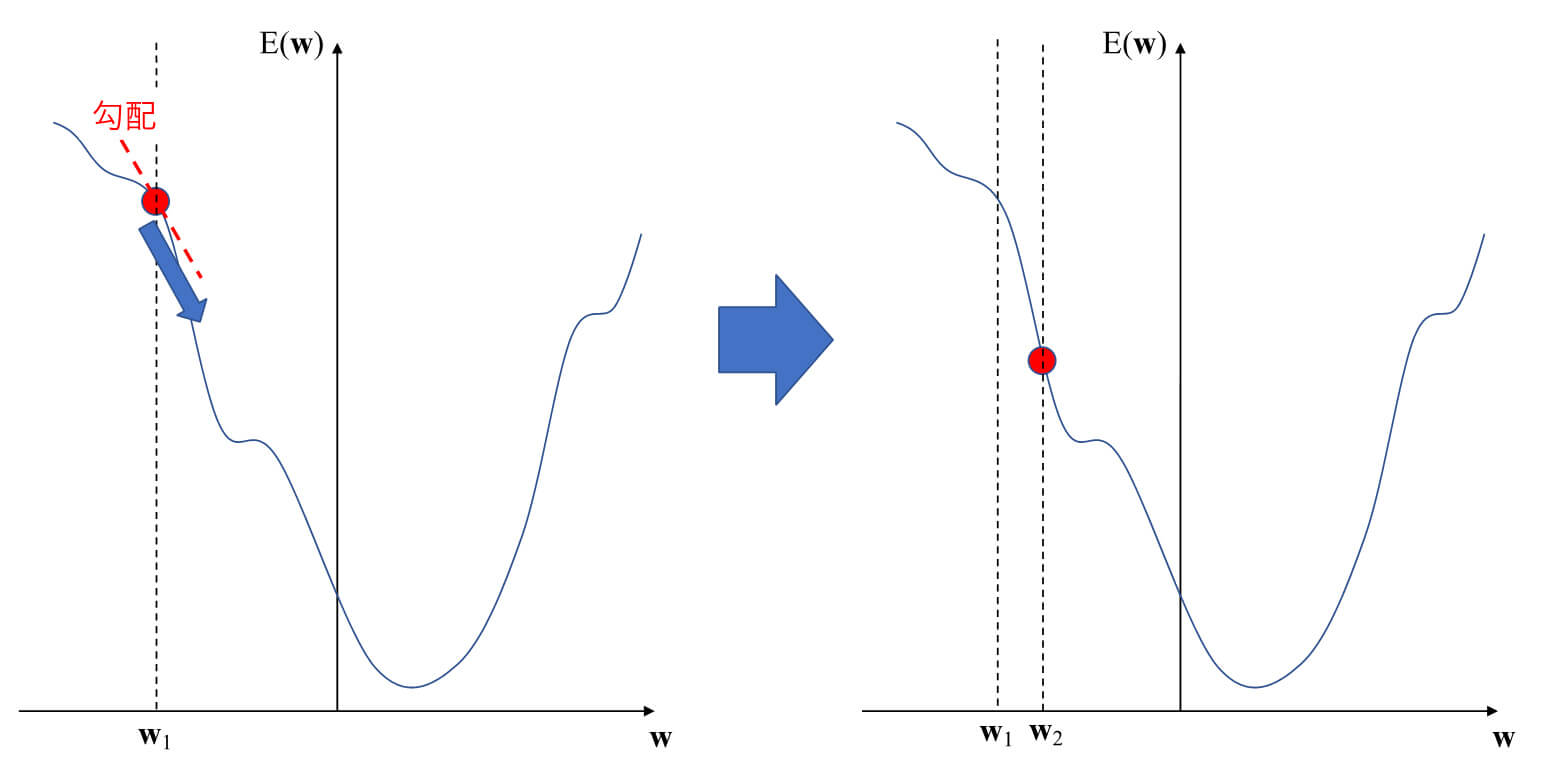
図1 勾配法
ニューラルネットワークにおける勾配法
図2に示すような、入力層のノードが10個、中間層のノードが20個、出力層のノードが5個のシンプルなネットワークを例に説明します。中間層のノードm1の値を求めるためには、入力層の全ノードからの入力値に対して重みw1(1,1),…w1(1,10)を掛けて総和を取り、b1(1)を足します。中間層のノードm2の値を求めるためには、入力層の全ノードからの入力値に対して重みw1(2,1),…w1(2,10)を掛けて総和を取りb1(2)を足します。同様に、出力層のノードy1の値を求めるためには、中間層の全ノードから出力層に入力される値に対し、重みw2(1,1),…w2(1,5)を掛けて総和を取りb2(1)を足します。
つまり、更新したい重みパラメータは入力層と中間層の間で10×20の200個、バイアスは20個となります。中間層と出力層の間は、重みパラメータが20×5の100個、バイアスは5個となります。これらの勾配を一度に計算することはできないため、1つのパラメータに着目しそれ以外のパラメータを固定する偏微分が必要となります。w1(1,1)を更新する場合は、w1(1,1)以外のパラメータを固定し、以下の通り値を更新します。ただし、損失関数をL(w)とし、αはパラメータの更新量です。
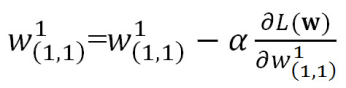
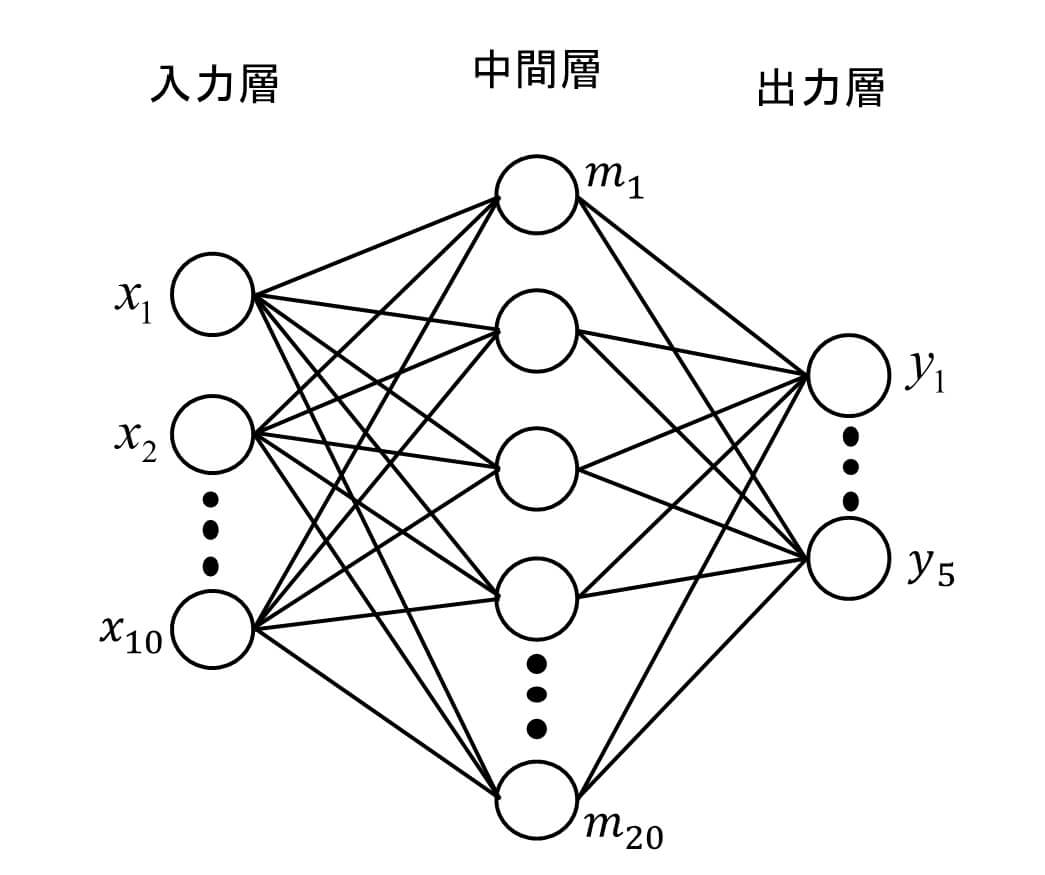
図2 ニューラルネットワーク
次回は、より効率的な「誤差逆伝搬法」による学習について説明します!
