第18回目の今回は、高精度な3次元計測に必要なサブピクセル推定について解説します。
OpenCVでは、対応点探索(ステレオマッチング)の関数内で自動的にサブピクセルを計算してくれますが、対応点探索を自分で実装する場合には、サブピクセル推定も合わせて実装するようにしましょう。
サブピクセル推定とは?
対応点探索では、画像の小領域をテンプレートとして、探索対象の画像上を1画素ずつ(または数画素ずつ)ずらしてスキャンしていくことで対応点を求めます(図1)。しかし、デジタル画像は画素が2次元に配置されたデータ構造なので、対応点の座標は整数値でしか求まりません。そこで、対応点の座標の小数値を推定する技術が必要となります。この技術がサブピクセル推定です。
サブピクセル推定では、対応点探索に用いる評価関数がSAD(Sum of Absolute Difference)のように一次関数であれば、等角直線フィッティングを用います。SSD(Sum of Squared Difference)のように二次関数であれば、パラボラフィッティングを用います。

図1 対応点探索
等角直線フィッティングとパラボラフィッティング
テンプレートと小領域間の一致度合を表す評価関数(SADとSSDの場合は誤差、NCCの場合は相関値)をF(d)とし、誤差が最小となった小領域の座標をdmin、その1画素前をdmin-1、1画素後をdmin+1とすると、図2に示すように等角直線フィッティングとパラボラフィッティングによりサブピクセル値(dsub)を求めることができます。
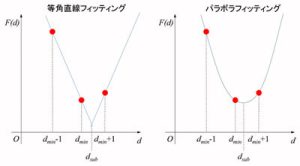
図2 等角直線フィッティングとパラボラフィッティング
ピクセルロッキング現象とその対策
実際にサブピクセルを推定した結果が、図3(左)です。図4の画像を0.1画素刻みでバイリニア法によりシフトした画像と、シフト前の画像の変位を、SSDとパラボラフィッティングを用いて求めた結果です(図4の画像は、ステレオマッチングの評価用データセットの画像です)。
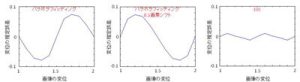
図3 パラボラフィッティングとEECによる推定誤差

図4 サブピクセル推定精度の評価に用いた画像
図3(左)をよく見ると、サブピクセルが0.5未満のときはマイナスの誤差が、0.5以上のときはプラスの誤差が発生していることが分かるかと思います。これがピクセルロッキング現象です。画像をバイリニア法によりシフトした画像の変位を求める、という理想的な条件下でも0.08pixel前後の誤差が発生してしまうわけです。
ピクセルロッキング現象の解決手段として、EEC(文献[1][2][3])という手法が提案されています。
EECでは図3(左)に示したサブピクセル推定結果に加え、対応点探索に用いる画像の一方(テンプレート画像、あるいは探索対象の画像)を0.5画素だけ平行移動した画像を生成し、SSDとパラボラフィッティングを用いてサブピクセルを推定します。
0.5画素平行移動することで、位相が真逆の誤差が発生します(図3(中))。つまり、図3(左)の結果と、図3(中)の0.5画素平行した画像を用いた結果の平均を取ることで、ピクセルロッキングが打ち消され、精度の高いサブピクセル推定結果を得ることができるのです(図3(右))。
EECを高速化する試みとして、0.5画素シフトした画像を生成せずに、dminの近傍±2画素分のdmin-2、dmin-1、dmin+1、dmin+2を用いて近似的に解を求める近似EECも提案されています。
サブピクセル推定について、ご理解いただけたでしょうか? 0.1画素以下の誤差が影響するような精度が求められる場合は、ピクセルロッキング現象の対策も取り入れてみてください。
次回は、動く1台のカメラで得られる画像系列から、画像中のシーンの3次元系列とカメラの位置を同時に計測する技術について解説します!
[1]清水, 奥富:“画像のマッチングにおける高精度なサブピクセル推定手法”, 電子情報通信学会論文誌, J84-D-II, 7, pp. 1409-1418 (2001).
[2] M. Shimizu and M. Okutomi: “Sub-pixel estimation error cancellation on area-based matching”, International Journal of Computer Vision, 63, 3, pp. 207-224 (2005).
[3] M. Shimizu and M. Okutomi: “Precise sub-pixel estimation on area-based matching”, Proc. ICCV 2001, Vol. 1, pp. 90-97 (2001).
